helloworld.cpp

Ceres solver 사용법 정리

이 글은 임형태님의 helloceres git 코드를 기반으로 작성되었습니다

Ceres solver를 사용하게 될 일이 있을 것 같아서 공부하면서 정리하면서 포스팅중이다

Ceres는 어떤 문제를 푸는가?

기본적으로 구속 조건이 있는 non-linear least square 문제를 풀 수 있다
ceres solver에 사용되는 기본 식의 뼈대는 아래 사진과 같다

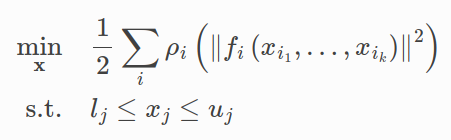
Example code

// A simple example of using the Ceres minimizer.
//
// Minimize 0.5 (10 - x)^2 using jacobian matrix computed using
// automatic differentiation.

#include "ceres/ceres.h"
#include "glog/logging.h"

using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solver;
using ceres::Solve;

// A templated cost functor that implements the residual r = 10 -
// x. The method operator() is templated so that we can then use an
// automatic differentiation wrapper around it to generate its
// derivatives.
struct CostFunctor {
    template<typename T>
    bool operator()(const T *const x, T *residual) const {
        residual[0] = 10.0 - x[0];
        return true;
    }
};

int main(int argc, char** argv) {
  google::InitGoogleLogging(argv[0]);

  // The variable to solve for with its initial value.
  double initial_x = 5.0;
  double x = initial_x;

  // Build the problem.
  Problem problem;

  // Set up the only cost function (also known as residual). This uses
  // auto-differentiation to obtain the derivative (jacobian).
  CostFunction* cost_function =
      new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);
  problem.AddResidualBlock(cost_function, nullptr, &x);

  // Run the solver!
  Solver::Options options;
  options.linear_solver_type = ceres::DENSE_QR;
  options.minimizer_progress_to_stdout = true;
  Solver::Summary summary;
  Solve(options, &problem, &summary);

  std::cout << summary.BriefReport() << "\n";
  std::cout << "x : " << initial_x
            << " -> " << x << "\n";
  return 0;
}

Break the code

CostFunctor

CostFunctor 구조체 안에 residual이 선언되어 있다

struct CostFunctor {
    template<typename T>
    bool operator()(const T *const x, T *residual) const {
        residual[0] = 10.0 - x[0];
        return true;
    }
};

이라고 선언하면 우리가 최소화 해야하는 함수는
\(\frac{1}{2} *(10 \, - \, x)^2\) 인 것을 알 수 있다

CostFunction/AutoDiffCostFunction

CostFunction* cost_function =
    new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);
problem.AddResidualBlock(cost_function, nullptr, &x);

위의 식에서 \(f\)에 해당하는 부분이다
cost function을 어떤 함수로 가져갈 지 선언해준다
이번 예제로는 \(f=(10-x)^2\) 이 되겠다

AutoDiffCostFunction이란 거 보니 자동으로 미분해주는? 그런 함수인 거 같은데 CostFunctor를 인자로 가져가는 걸 봐서 저걸 사용하겠다까지는 이해했는데, 그 뒤에 들어가는 숫자 인자자인 <Costfunctor, 1, 1> 부분은 좀 더 스터디가 필요하다

AddResidualBlock

problem.AddResidualBlock(cost_function, nullptr, &x);

인자가 넘어가는 형태로 보아 위에서 정의했던 cost_function \(f\) 를 최소화 하는 파라미터 \(x\)를 찾아야 하니까 그런 residual block 하나를 추가하겠다라는 뜻 인 거 같다!

Solver

solver를 선언하기 전에 options를 먼저 선언해주고, solver의 option들을 넣어준다

Solver::Options options;
  options.linear_solver_type = ceres::DENSE_QR;
  options.minimizer_progress_to_stdout = true;
  Solver::Summary summary;
  Solve(options, &problem, &summary);

는 최소화 하는 과정을 출력할 지 말 지 결정하는 파라미터로 추정된다.

Solver()함수를 통해서 문제를 풀어준다

• 우리가 residual block 하나를 넣었던 problem
• 방금 정의한 solver의 option
• 최소화 과정을 요약한 summary 이 세 인자를 넘겨주고 문제를 풀 수 있게 된다
  

결과

\(f=(10-x)^2\) 이었으므로 우리는 손으로도 \(x=10\)을 구할 수 있고,
ceres solver 결과도 동일함을 확인했다

iter      cost      cost_change  |gradient|   |step|    tr_ratio  tr_radius  ls_iter  iter_time  total_time
   0  1.250000e+01    0.00e+00    5.00e+00   0.00e+00   0.00e+00  1.00e+04        0    4.98e-05    1.13e-04
   1  1.249750e-07    1.25e+01    5.00e-04   5.00e+00   1.00e+00  3.00e+04        1    7.61e-05    3.02e-04
   2  1.388518e-16    1.25e-07    1.67e-08   5.00e-04   1.00e+00  9.00e+04        1    1.79e-05    3.43e-04
Ceres Solver Report: Iterations: 3, Initial cost: 1.250000e+01, Final cost: 1.388518e-16, Termination: CONVERGENCE
x : 5 -> 10

최소자승법으로 문제를 풀기 때문에 iteration이 여러번 들어가는데, 이번 예제에서는 2번 만에 \(x=10\)으로 수렴하였다

Reference

• LimHyungTae/helloceres