[자료 구조 #6] 알고리즘 복잡도

기회는 준비된 자에게 온다 !

시간 복잡도의 정의

시간 복잡도(Time Complexity)란 알고리즘이 문제를 해결하기 위한 연산의 횟수다.

알고리즘을 평가할 때 2가지의 척도가 사용된다.

복잡도니까 낮을 수록 효율적인 알고리즘이겠지? 라는 생각을 해본다.

이를 정량적으로 표현하기 위해 빅오 표기법을 사용한다.

시간 복잡도의 경우 빅오(Big-O)로 표현한다.

통상 연산 횟수를 카운팅 할 때는 3가지를 사용한다.

따라서 빅오 표기법이란 최악의 경우를 고려하여, 프로그램이 실행되는 과정에서 소요된 연산 횟수를 카운팅한다.

아래는 자주 사용되는 빅오 표기법의 표와 그래프이다.

빅오 표기법	표현	설명
\(\mathbf{O}(1)\)	상수	프로그램에서 라인 한 개가 실행되는 경우
\(\mathbf{O}(logN)\)	로그	입력 데이터의 크기가 커질수록 처리 시간이 로그만큼 줄어 들 때, 이진 탐색이 대표적, 재귀가 순기능으로 이루어질 때
\(\mathbf{O}(N)\)	선형	입력에 비례하여 처리 시간이 증가할 때. 즉, 반복문이 N번 반복할 때
\(\mathbf{O}(NlogN)\)	로그 선형	데이터가 많아질수록 로그배만큼 늘어나는 알고리즘. 정렬 알고리즘 (퀵, 병합 정렬)이 대표적
\(\mathbf{O}(N^2)\)	다항	데이터가 많아질수록 처리 시간이 급수적으로 늘어날 때, 이중 반복문이 대표적
\(\mathbf{O}(2^n)\)	지수	데이터량이 많아질수록 처리시간이 기하급수적으로 늘어나는 경우, 피보나치 수열과 재귀가 역기능을 할 경우가 대표적

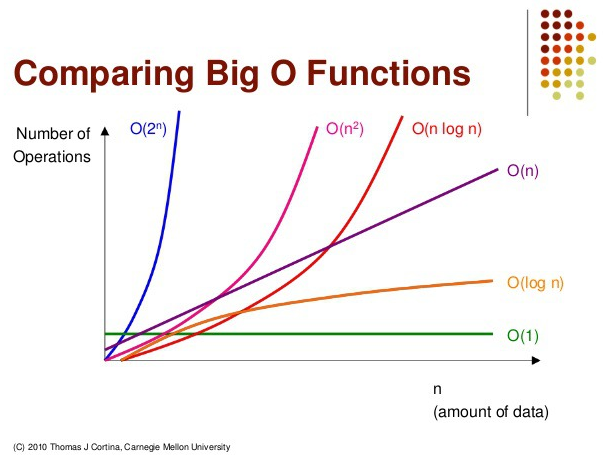
여기서 N이란 입력되는 데이터의 개수를 의미한다 !

적은 연산으로도 같은 동작을 하는 알고리즘이 효율적인 알고리즘이다.

시간 복잡도를 줄이기 위한 다양한 방법이 있다.

그 중 대표적인 방법은 1) 반복문의 사용을 줄이는 것과 2) 자료 구조를 적절히 사용하는 것 그리고 3) 알려진 알고리즘을 적절히 사용하는 것이다.

고맙게도 좋은 테이블이 있다.

위로 갈수록 알고리즘이 빨라지고 아래로 갈수록 속도가 감소한다.

입력 데이터 N=10,000일 때 O(n^2)의 경우 1억 번의 연산을 수행하게 된다.

이 때 CPU가 1억 번의 연산을 수행하는데 1초가 걸린다고 가정하면, 해당 데이터에 대해서는 O(n^2) 알고리즘에 대해 1초가 소요된다고 예측할 수 있다.

공간 복잡도(Space Complexity)는 작성한 프로그램이 얼마나 많은 공간(메모리)를 차지하느냐를 분석하는 방법이다.

컴퓨팅 성능이 좋을 때는 시간 복잡도에 비해 주요 고려 대상이 아니지만 제한된 컴퓨팅 자원에서는 이마저도 중요한 요소이다.

하지만 코딩테스트의 경우 시간 복잡도를 우선시해도 될 것 같다?.. 따라서 공간 복잡도는 나중에 필요할 때 공부하도록 하자.